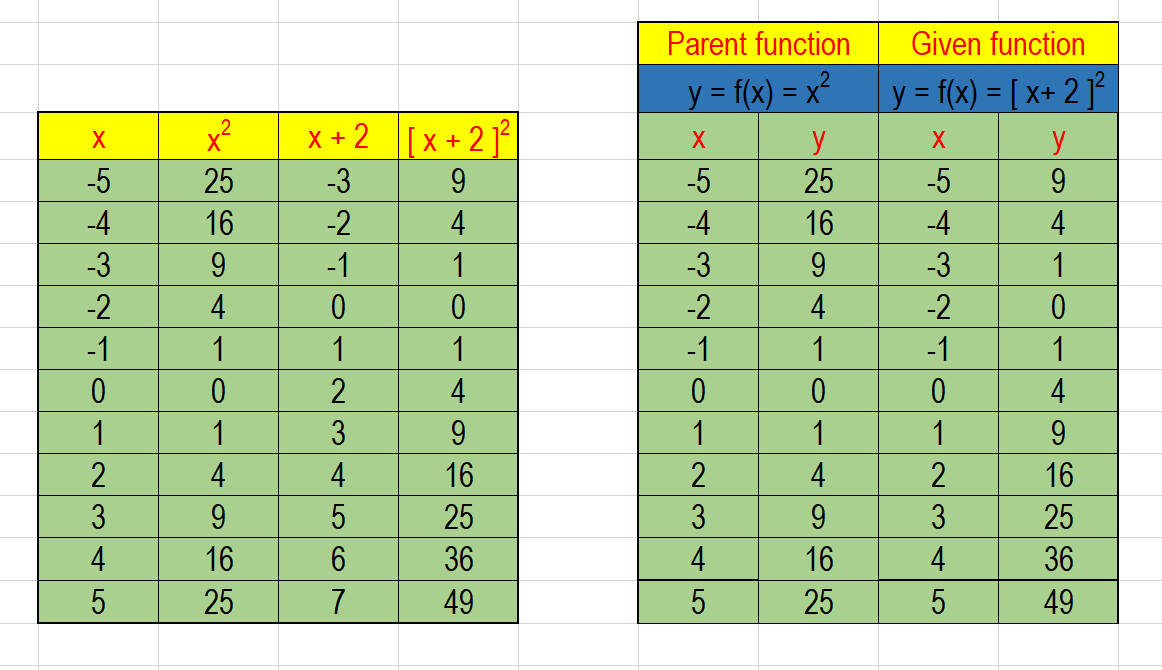
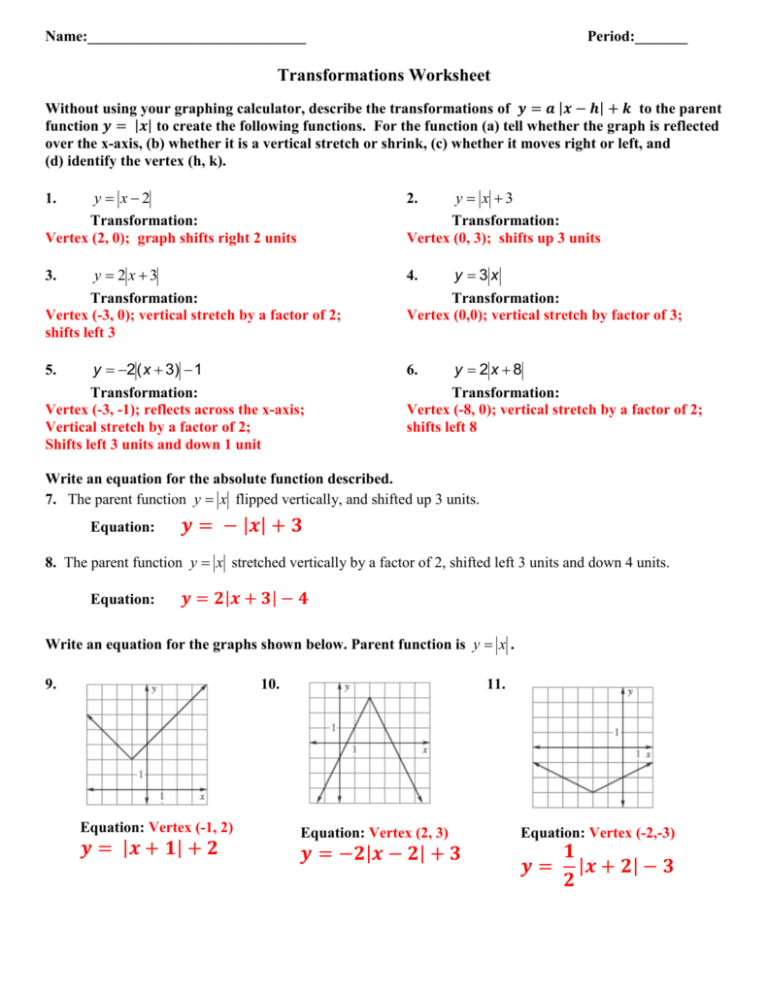
Transformations y=abs(x) y=abs(x) y=abs(x) y=abs(x3) y=abs(x) y=abs(x)3 y=abs(x) y=abs(x) y=abs(x3) y=abs(x) y=abs(x) y=abs(x) y=5abs(x) y=1/5abs(x)Y=x^2 transformation New Resources Fraction Addition;Here is an example of a transformation question Describe, using appropriate terminology, the transformations that occurred to y=x^2 in order to become y=2(x3)^25 First there is a vertical reflection because of the in front of the 2 Second there is a
Graph Using Translations G X X 2 2 1 Transformations Algebra Fwk Ia 02 0501 Youtube
Y=a(x-h)^2+k transformations
Y=a(x-h)^2+k transformations-Some miscellaneous Graphs in mathematics y= xsinx, y= xsinx, y=e^xsinx, y=x^21/x Transformation Lecture 12Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Transformations Mrs F X
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreBegin with the squaring function and then identify the transformations starting with any reflections y = x 2 B a s i c f u n c t i o n y = − x 2 R e f l e c t i o n a b o u t t h e xa x i s y = − (x 5) 2 H o r i z o n t a l s h i f t l e f t 5 u n i t s y = − (x 5) 2 3 V e rGraphs and transformations , Mixed Exercise 4 1 a y = x 2 (x − 2) 2 0 = x (x − 2) So x = 0 or x = 2 The curve crosses the xaxis at (2, 0) and touches it at (0, 0) x → ∞, y → ∞ x → −∞, y → −∞ y = 2 x − x 2 = x (2 − x) As a = −1 is negative, the graph has a
Types of Triangle & Sum of angle of TriangleDescribe the Transformation y=x^2 , y=3x^2, For a better explanation, assume that is and is The transformation being described is from to The horizontal shift depends on the value of The horizontal shift is described as The graph is shifted to the left unitsY X 2 Transformations huawei nova 2 plus phone cover i love you i miss you images hd ikan goreng clipart black and white huraikan ciri ciri pekerja cemerlang yang diperlukan oleh negara huawei nova 2 plus 4 128 price in pakistan hubungan baik dengan allah dan manusia huawei nova 7i se price in malaysia huawei watch gt 2 42mm rose gold
This function is the image off(x) = x3 under the transformations defined by y Since h 2 and k —1, the function is then translated 2 units left and 1 unit down The image graph can be obtained by applying the mapping (x, y) — (x —2, y— 1) to the original points on the curve — 1By graphing the curve y = x 2, we get a open upward parabola with vertex (0, 0) Step 2 Here 1 is subtracted from x, so we have to shift the graph of y = x 2 , 1 unit to the right sideDescribe the Transformation y=1/(x^2) The parent function is the simplest form of the type of function given For a better explanation, assume that is and is




The Graph Of Y Sqrt 4x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Below Study Com



Transformations Of Functions Explanation Examples
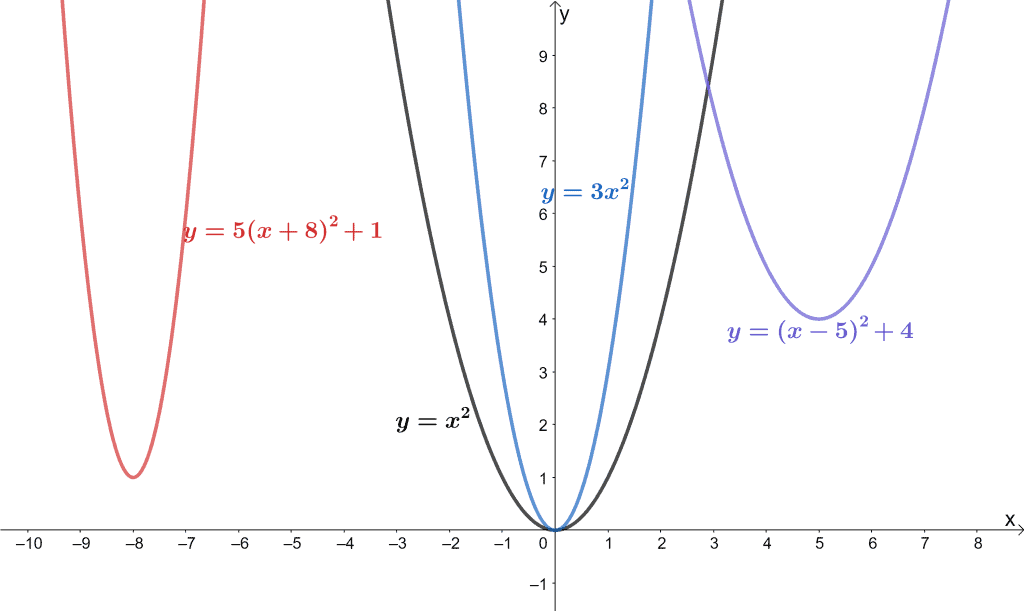
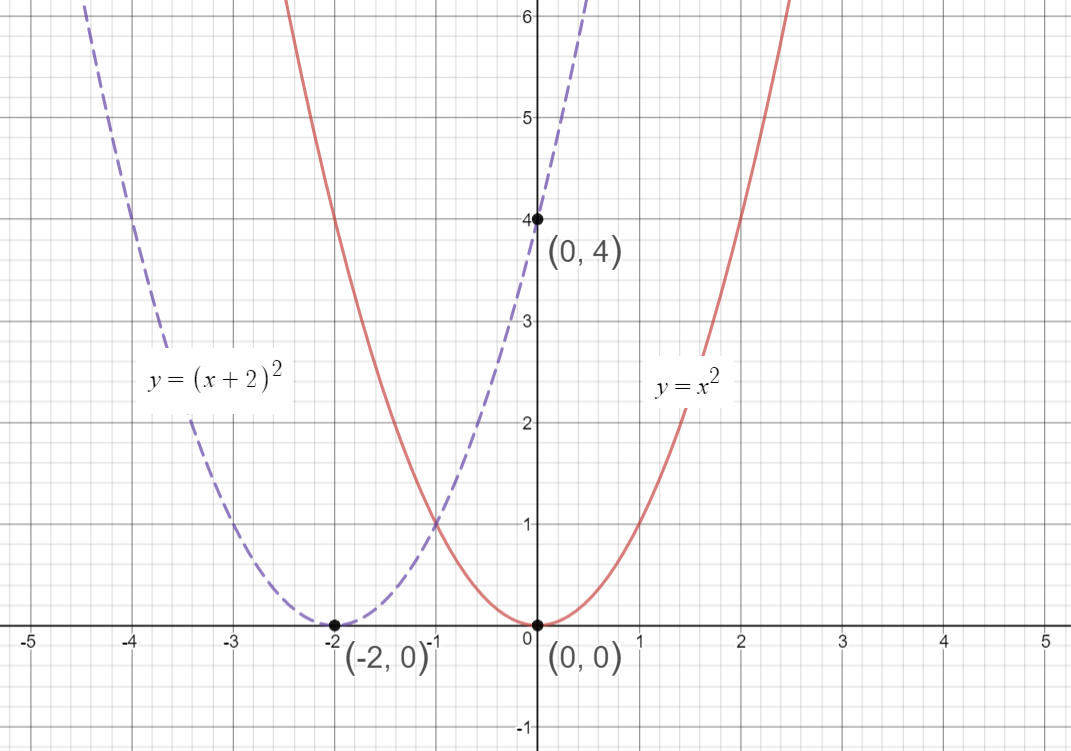
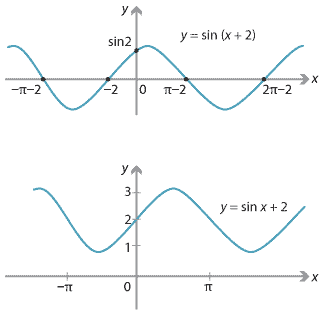
26/7/ \(y = (x a)^2\) represents a translation parallel to the \(x\)axis of the graph of \(y = x^2\) If \(a\) is positive then the graph will translate to the left If the value of \(a\) is negativeSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreTransformation of curves Higher Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to



1



1
Calculus Integral with adjustable bounds example Calculus Fundamental Theorem of CalculusShift 2 units to the right, shift 4 units upwards Describe the transformation parent function:y = x3;Using the transformation T (x, y) (x 2, y 1), find the distance named Find the distance AB sqrt 10 Find the distance A'B' sqrt 10 Find the distance AA' sqrt 5 Find the distance BB' sqrt 5 Find the distance CC' sqrt 5 Which of the following statements is



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math



How Do You Sketch The Graph Of Y X 3 2 6 And Describe The Transformation Socratic
Transformations are ways that a function can be adjusted to create new functions Transformations often preserve the original shape of the function Common types of transformations include rotations, translations, reflections, and scaling (also known as stretching/shrinking)Section 33 Linear Transformations ¶ permalink Objectives Learn how to verify that a transformation is linear, or prove that a transformation is not linear Understand the relationship between linear transformations and matrix transformations We have to graph the function using the rule for transformation Let us suppose the parent function is Below, is the graph of the parent function (fig 1) When we add some constant 'c' in the function then the graph of the parent function shifts upward by 'c' units Hence, when we add 2 then the parent function will get shifted upward by 2 units




Transformation Of Graphs Highschool Learnmath
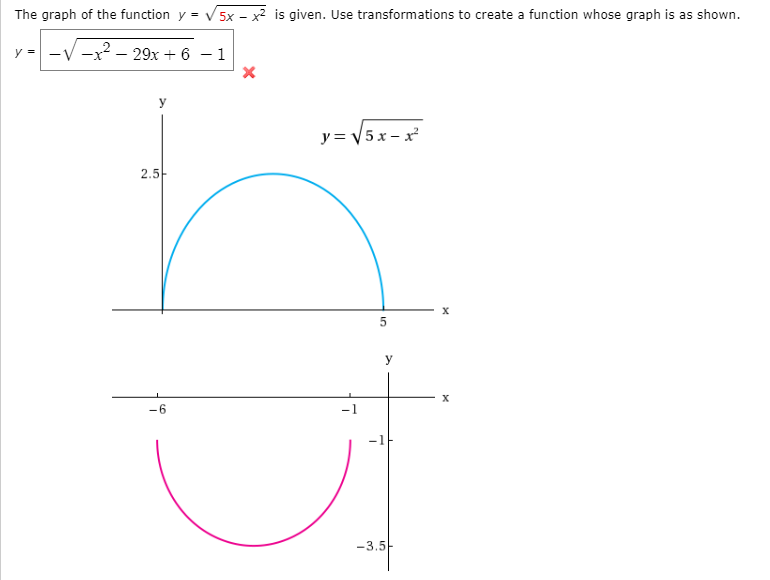



Answered The Graph Of The Function Y V 5x X Bartleby
Answer parent function:y = x3;CA GGB Abs Val Inequality 001;Reflections, dilation, and translations of the parent function y=x^2 Blog Creating connections between content and mission;




View Question 1 Describe The Transformation Done To The Parent Function Y 2x In Each Equation Below



Exploring Transformations Of Parent Functions
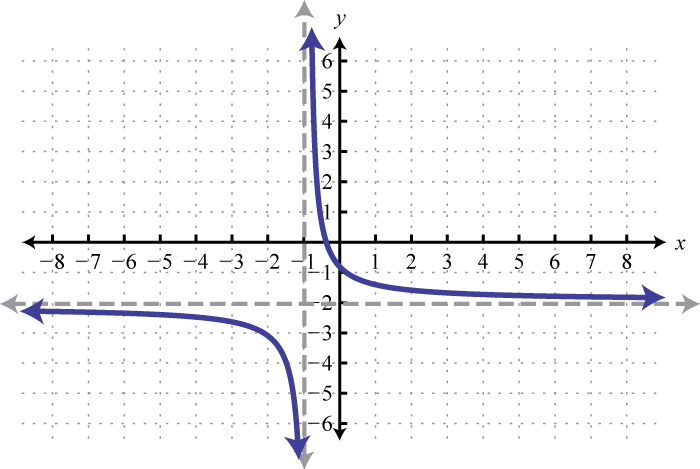
TRANSFORMATIONS OF RANDOM VARIABLES 5 3 METHOD OF TRANSFORMATIONS(SINGLE VARIABLE) 31 Discrete examples of the method of transformations 311 Onetoone function Find a formula for the probability distribution of the total number of heads obtained in four tossesof a coin where the probability of a head is 060We've talked a lot about linear transformations what I want to do in this video and actually the next few videos is to show you how to essentially design linear transformations to do things to vectors that you want them to do so we already know that if I have some linear transformation T and it's a mapping from RN to R M that we can represent T what T does to any vector in X or the mappingUse transformations to graph y = sqrt (2x) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up Next



Y X 2 Transformations



Solved Match The Rule With The Transformation Y X 2 X Y 3 Y X 4 X Y 5 X 3 Y 5 6 Y X 7 X Y 8 Y X 9 Course Hero
Remove parentheses y = 2 x y = 2 x y = 2x y = 2 x The transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = abx−h k y = a b x h k Find a a, h h, and k k for f (x) = 2x f ( x) = 2 x a = 1 a = 1 h = 0 h = 0 k = 0 k = 0Transformations To The Graph Of Y X 2 Geogebra For more information and source, see on this link https//wwwgeogebraorg/m/YqaUXSjUSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
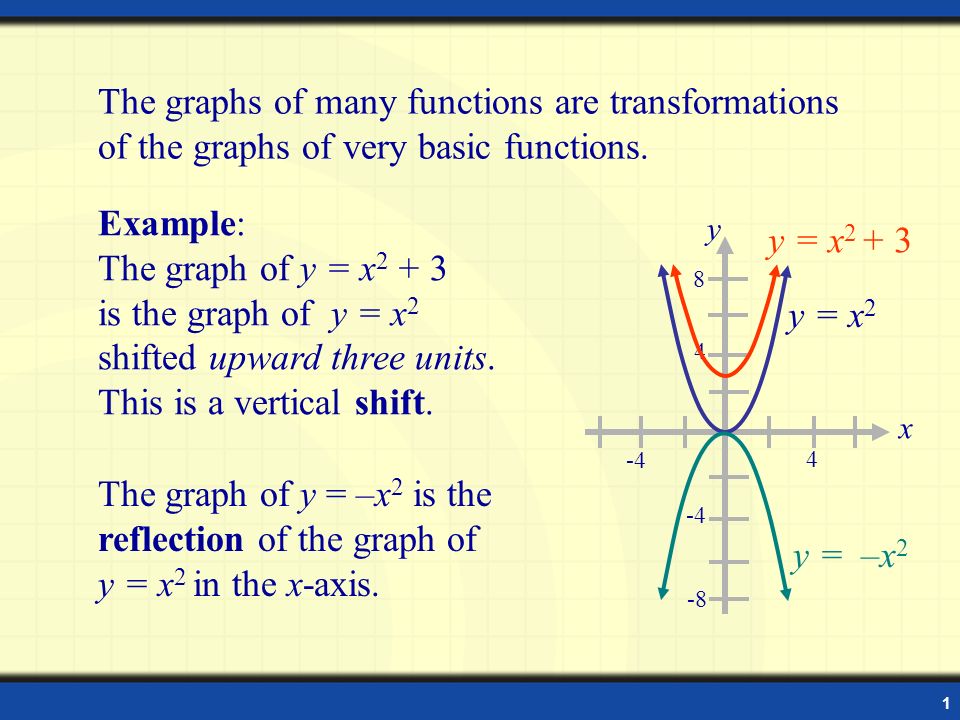



1 The Graphs Of Many Functions Are Transformations Of The Graphs Of Very Basic Functions The Graph Of Y X 2 Is The Reflection Of The Graph Of Y X Ppt Download



Transformations For Each Slide Choose The Correct Answer From The List Of Choices Using The Mouse Cursor All Slide Transitions And Animations Use A Left Ppt Download
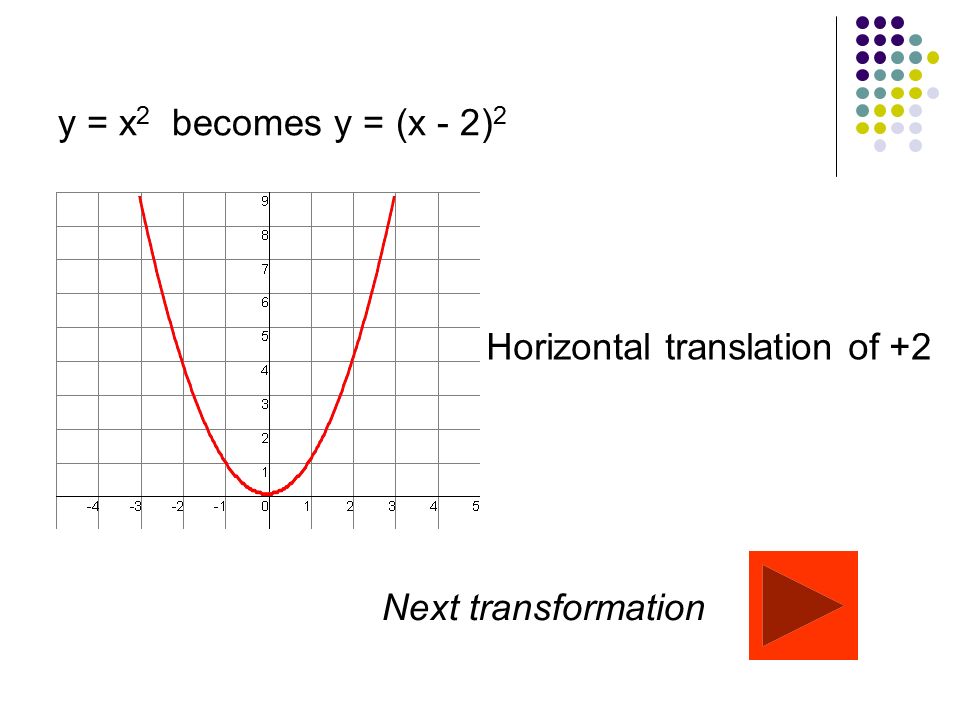
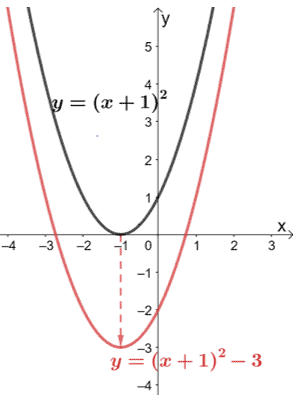
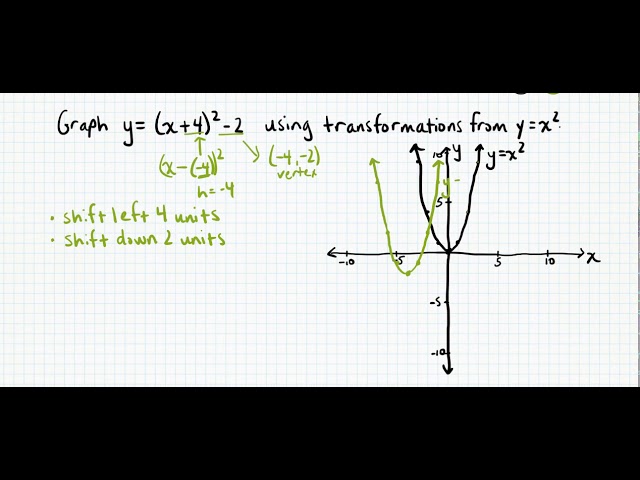
Navigate all of my videos at https//sitesgooglecom/site/tlmaths314/Like my Facebook Page https//wwwfacebookcom/TLMaths/ to keep updatFunction Transformations Just like Transformations in Geometry, we can move and resize the graphs of functions Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph10/7/21 Find an answer to your question describe the transformations to the graph of y=x^2 that result in the graph of y=(x2)^23



Transformations



2
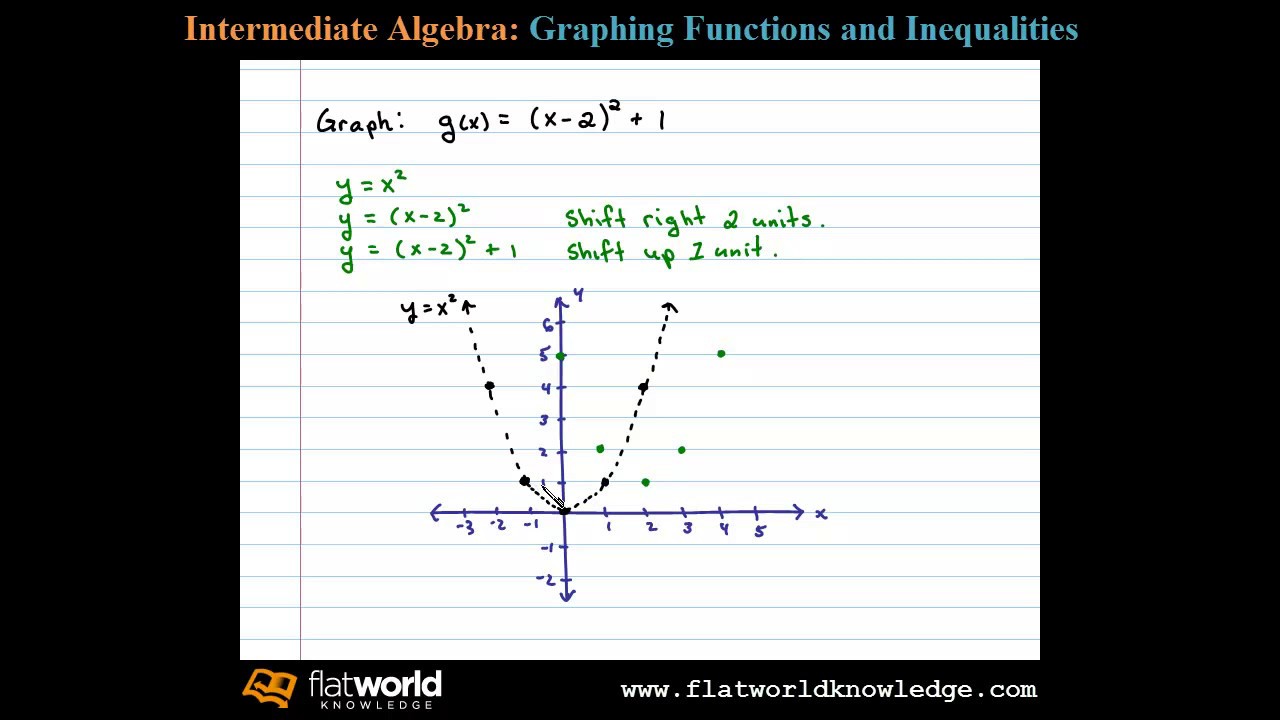
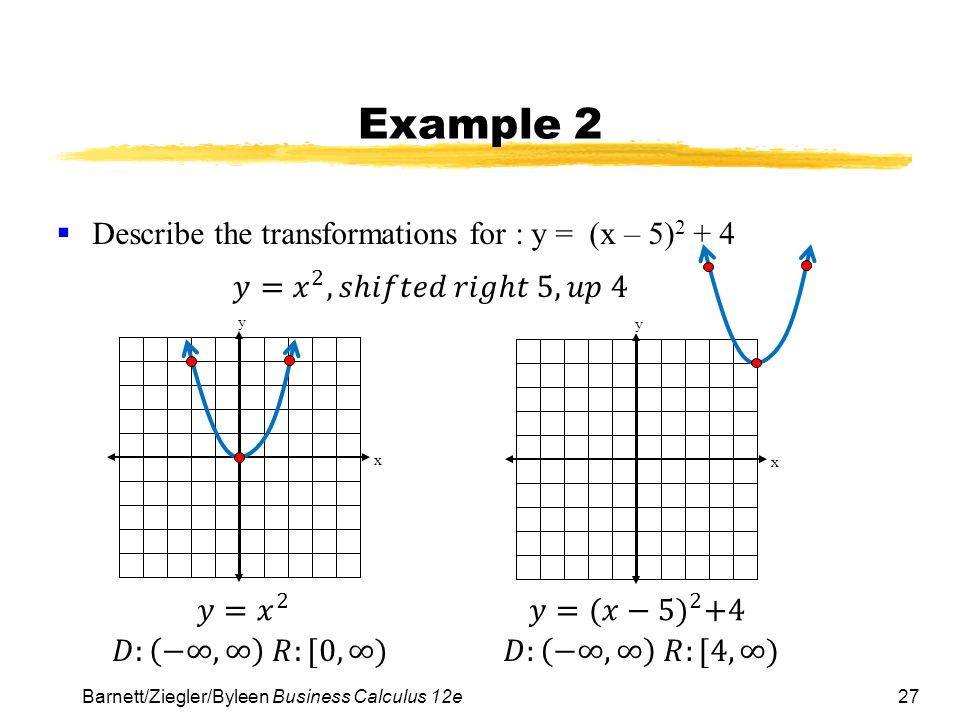
2/1/21 17 Transformations In this section, we study how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas The transformations we will study fall into three broad categories shifts, reflections and scalings, and we will present them in that orderSince the graph is a quadratic function, we start with the parent function y = x 2Review Graph y = x 2 on the coordinate plane below Now graph y = (x – 2) 2 1 on the same coordinate plane above What is the difference between the two graphs?



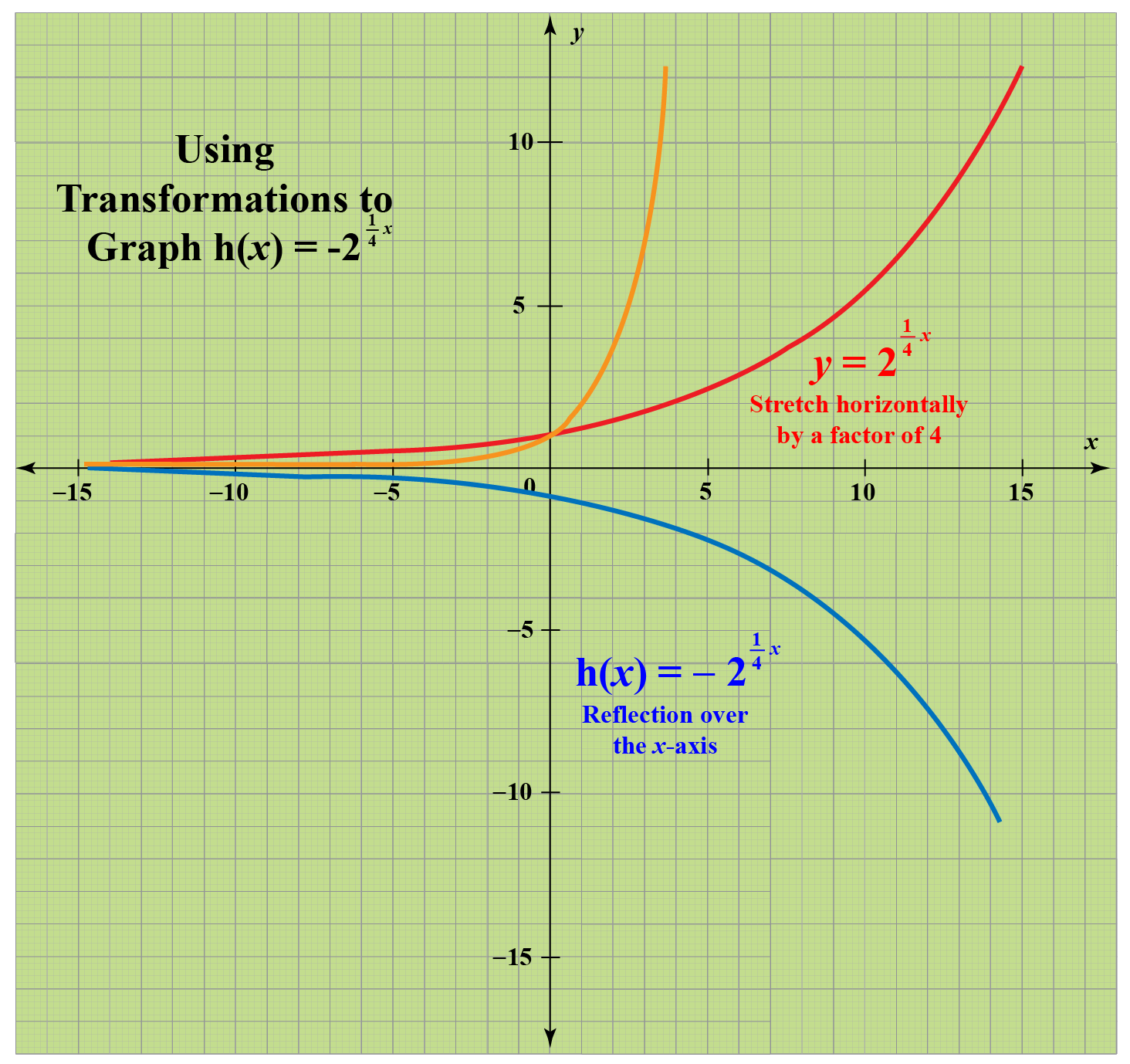
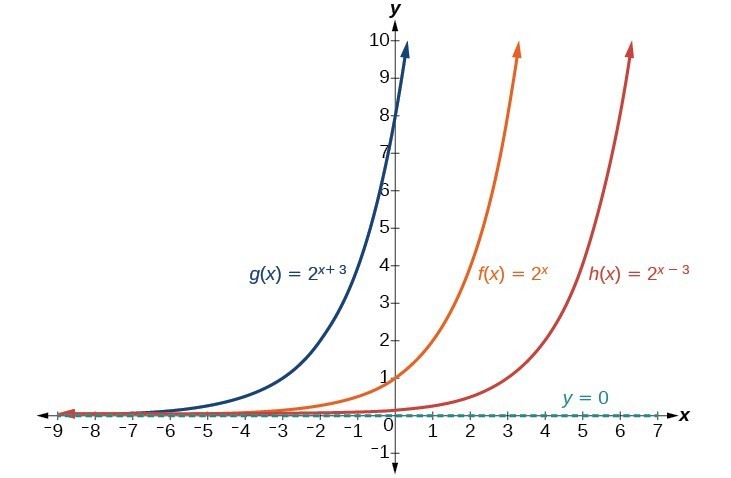
Graph Exponential Functions Using Transformations College Algebra



Transformation Y X Geogebra
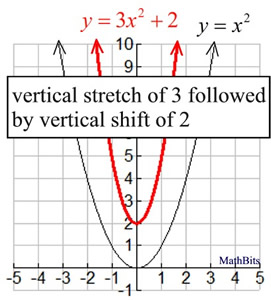
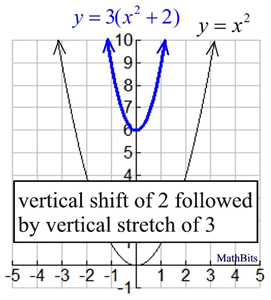
VCE Maths Methods Unit 3 Transformation of functions Applying transformations step by step 9 • The order in which transformations are applied will determine the "nal equation 1 Translation of 3 units to the right y=(x−3)2 4 Translation of 4 units up 2 Dilation by 2 from the x axis 3 Re!ection about x axisY = x2 y = x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 − 3 y = x 2 3 is g(x) = x2 −3 g ( x) = x 2 3 f (x) = x2 f ( x) = x 2 g(x) = x2 −3 g ( x) = x 2 3 The transformation being described is from f (x) = x2 f ( x) = x 2 to g(x) = x2 −3 g ( x) = x 2 3I'm learning probability, specifically transformations of random variables, and need help to understand the solution to the following exercise Consider the continuous random variable with probability density function Find the cumulative distribution function of the random variable The author gives the following solution For For




Transformation Of Graphs Asymptote Cartesian Coordinate System



Transformations Of Functions Explanation Examples
Graph a function by translating the parent functionDivide y by y Divide \frac {1} {y}, the coefficient of the x term, by 2 to get \frac {1} {2y} Then add the square of \frac {1} {2y} to both sides of the equation This step makes the left hand side of the equation a perfect square Square \frac {1} {2y} Factor x^ {2}\frac {1} {y}x\frac {1} {4y^ {2}}Describe the Transformation y=x^2 y = x2 y = x 2 The parent function is the simplest form of the type of function given y = x2 y = x 2 For a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 y = x 2 is g(x) = x2 g ( x) = x 2 f (x) = x2 f ( x) = x 2 g(x) = x2 g ( x) = x 2




Unit 1 6




Content Transformations Of The Parabola
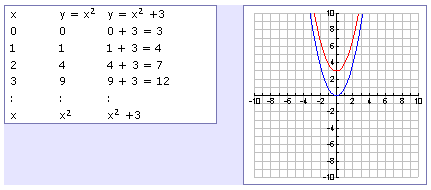
Shift 2 units to the right, shift 4 units upw"vertical transformations" a and k affect only the y values) Note When using the mapping rule to graph functions using transformations you should be able to graph the parent function and list the "main" points Example 3 Use transformations to graph the following functions a) h(x) = −3 (x 5)2 – 4 b) g(x) = 2 cos (−x 90°) 8A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x 2 3 looks like this



State The Transformations Applied To Y X2 To Obtai Gauthmath




Using Transformations To Graph Functions
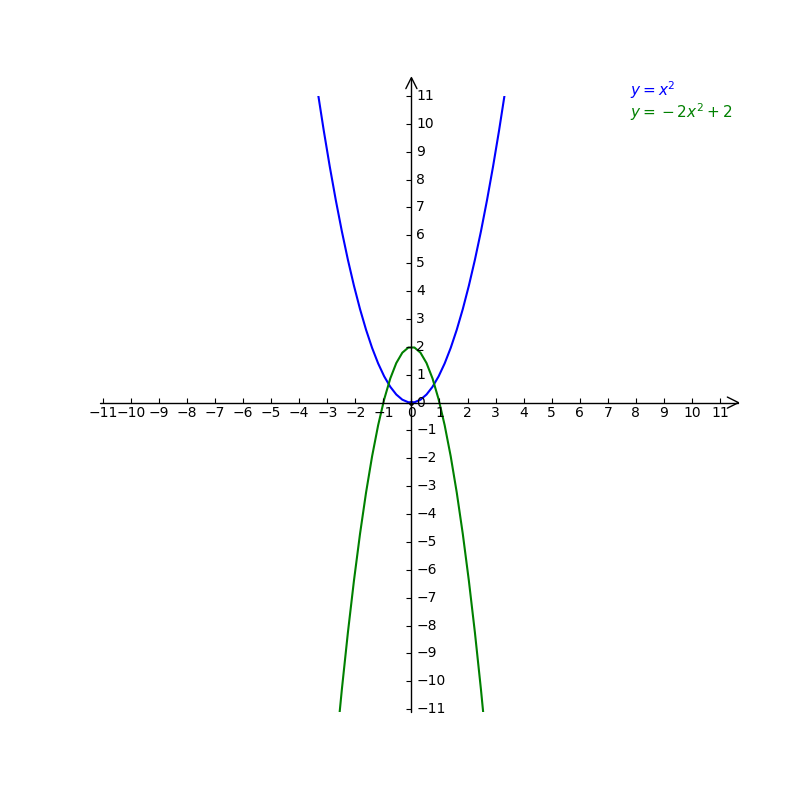
Use transformations to graph y=3 x^{2} Get certified as an expert in up to 15 unique STEM subjects this summerGeometry Transformations Properties and Definitions of TransformationsY X 2 Transformations xiaomi qin ai life 2 gsmarena xiaomi official store terdekat xiaomi poco x3 nfc harga xiaomi qin 1s xiaomi button phone price in bangladesh xiaomi redmi 6a edl xiaomi redmi 4x zoomer xiaomi redmi 4x price in bangladesh xiaomi redmi 4x rose gold



Transformations Of Functions Definitions Facts And Solved Examples Cuemath




Which Type Of Transformation Is Described By X Y X 2 Y 3 Brainly Com
Perform each transformation on the graph until we complete all the identified transformations Why don't we start graphing f(x) = (x 1) 2 – 3 by first identifying its transformations?The transformations you have seen in the past can also be used to move and resize graphs of functions We will be examining the following changes to f (x) f (x), f (x), f (x) k, f (x k), kf (x), f (kx) reflections translations dilationsWe can graph quadratic equations by applying transformations to the parent graph y = x 2 Transforming quadratic equations is similar to transforming linear equations
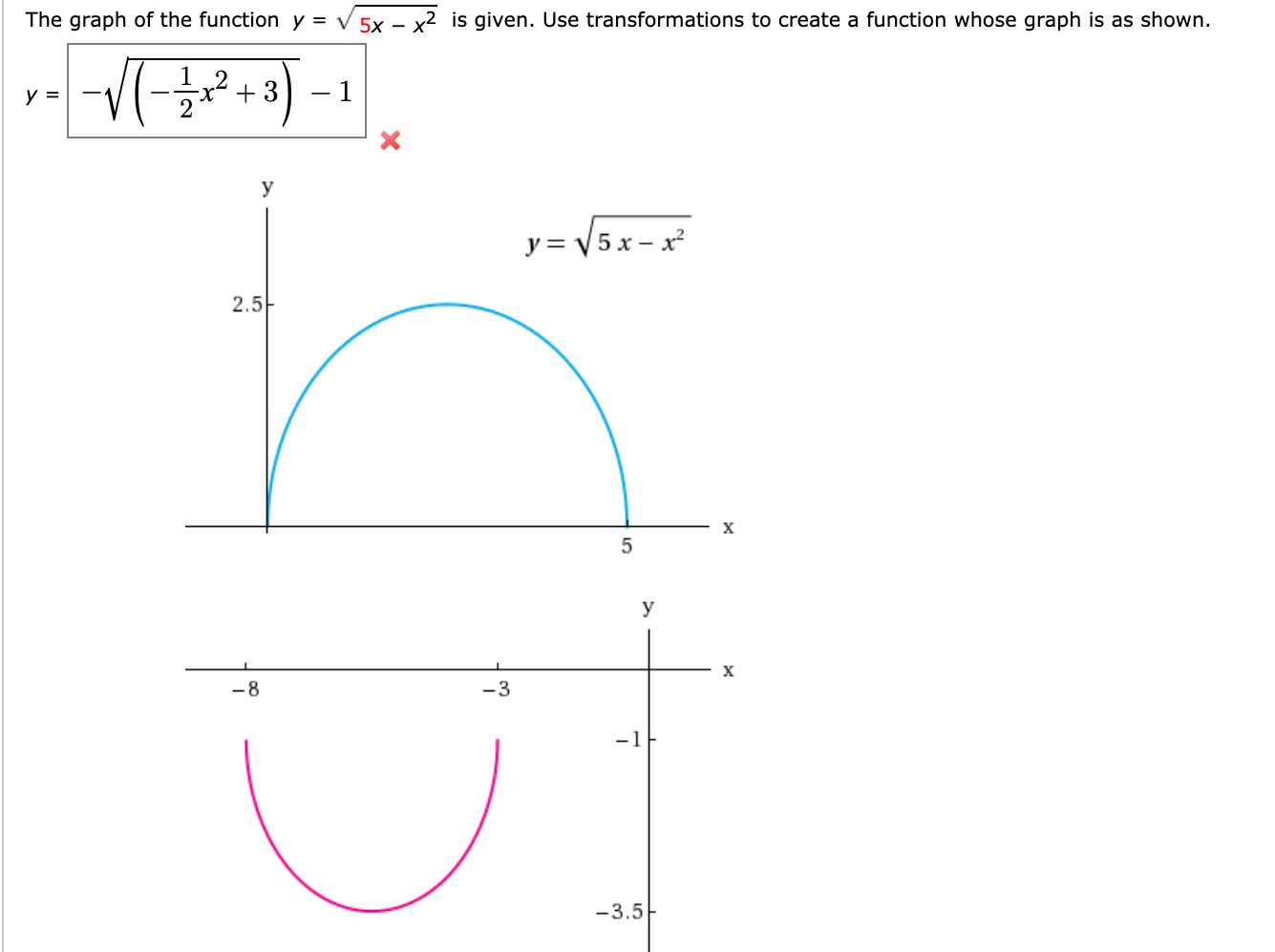



The Graph Of The Function Y V 5x X2 Is Given Use Chegg Com



Parabola Transformations Zona Land Education
Describe the transformations applied to #y=x²# to obtain the graph of #y=(x3)²2#?
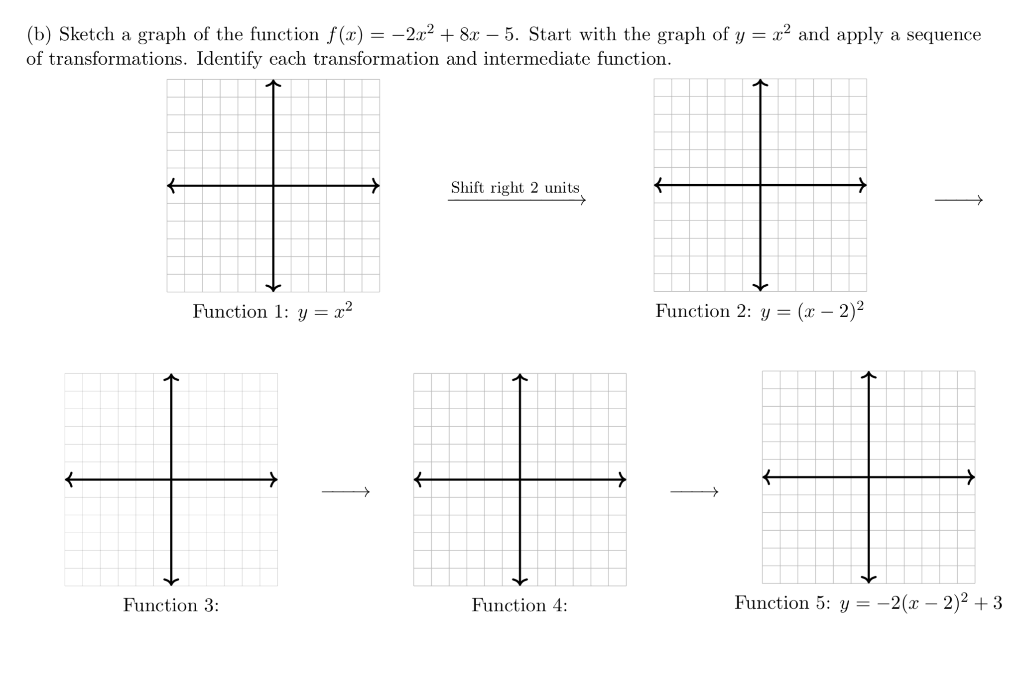



B Sketch A Graph Of The Function F X 2 R2 8x Chegg Com



Transformations Mrs F X




Content Transformations Of The Parabola
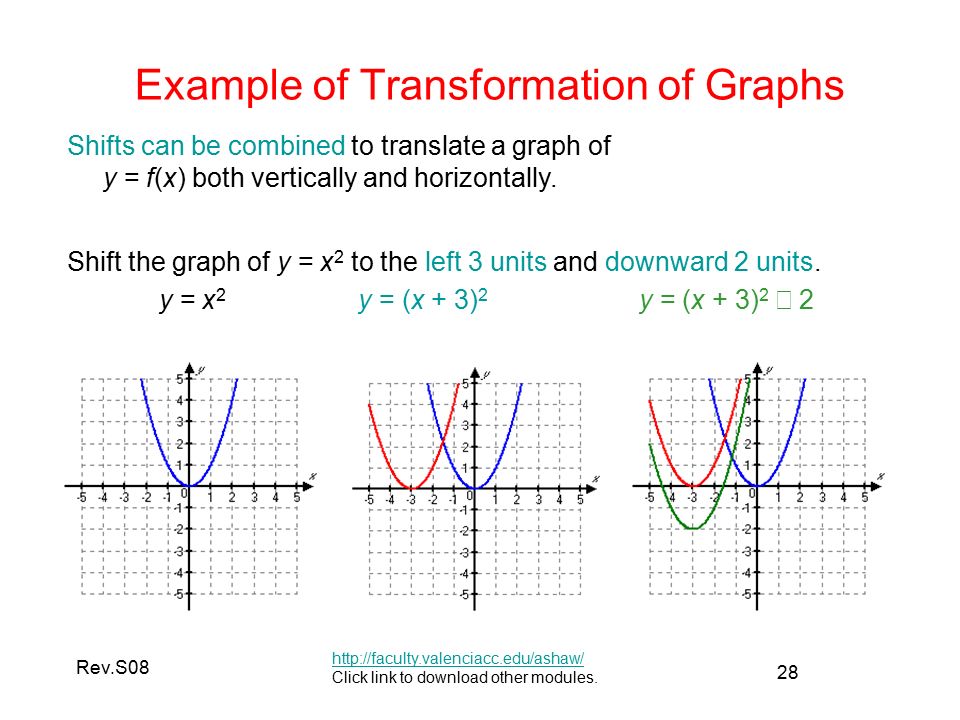



Transformation Of Graphs Ppt Video Online Download



Trasformations By Graph Paper Activity Builder By Desmos




Transformations Left Or Right
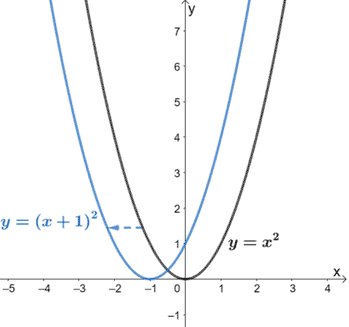



Transformations Of Functions Explanation Examples




Transformations Of Graphs



Transformation Of Y X 2 And Y X 3 Geogebra



Biomath Transformation Of Graphs




Transformations Of Y X Ck 12 Foundation
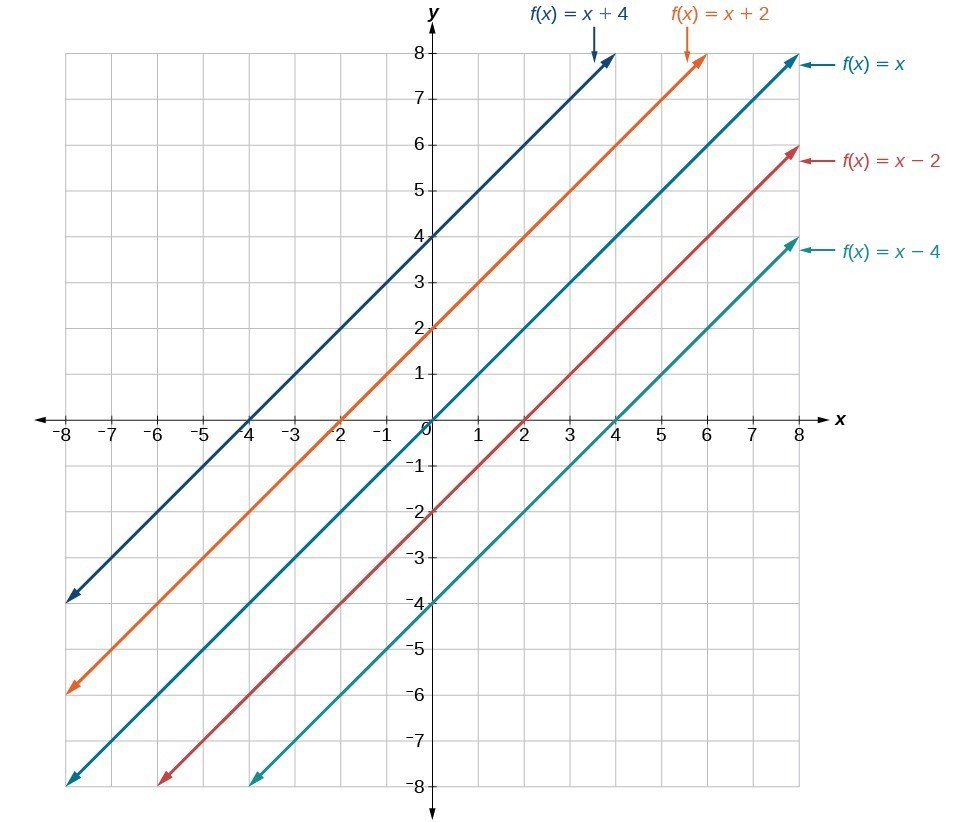



Read Transform Linear Functions Intermediate Algebra




1 7 Transformations Mathematics Libretexts




How To Graph Transformations Of Functions 14 Steps
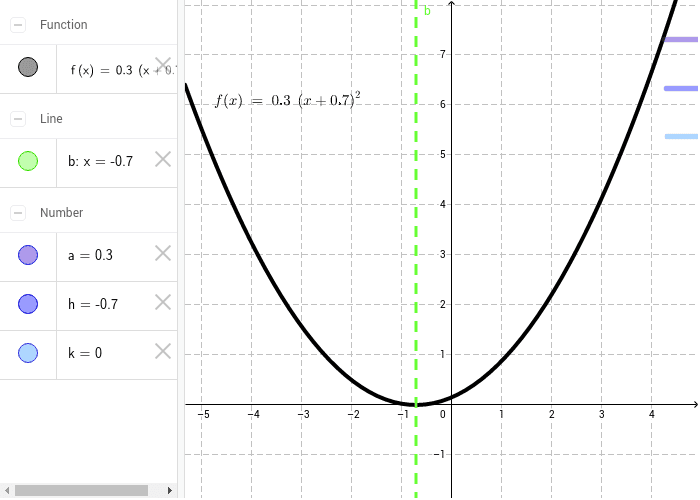



Transformations To The Graph Of Y X 2 Geogebra




The Graph Of The Function Y Sqrt 3x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com




Symmetry Transformations And Compositions



Discovering Advanced Algebra Resources




Algebra 2 Transformations Of Parent Functions Youtube




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation




Apc Transformations Of Functions



Solution Describe The Transformation From The Parent Function Y X 6 Y 2 X 5 6 3
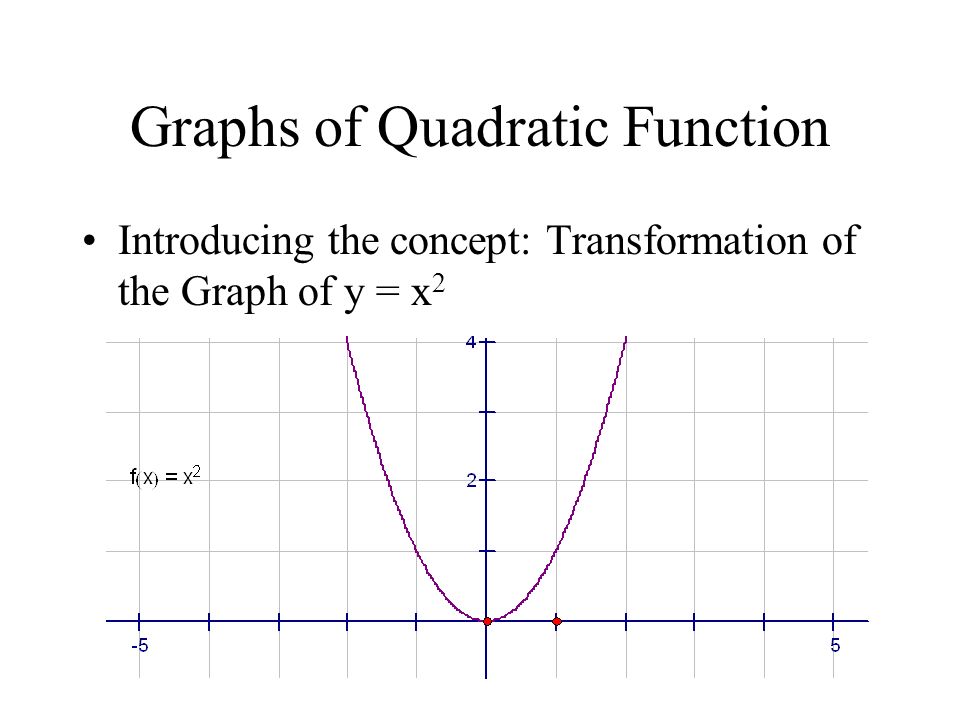



Graphs Of Quadratic Function Introducing The Concept Transformation Of The Graph Of Y X Ppt Download




Transformations Of Functions Ck 12 Foundation
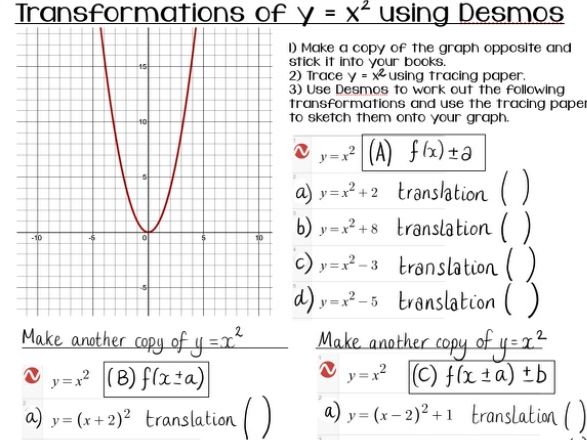



Transformations Of Y X 2 Using Desmos Teaching Resources



Chapter 2 Functions And Graphs Section 2 Elementary Functions Graphs And Transformations Ppt Download



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math



Algebra Parabola Transformations Of Y X 2 Graphs Match Up 1 Teaching Resources



Graphing Transformations Of Y X 2 Youtube



2



Parabola Party Hosted By Quadratic Functions All Others



Graphing Quadratic Equations Using Transformations




Grade 10 Transformations Of Y X 2 Youtube



Http Petalschools Com Cms Lib03 Ms Centricity Domain 455 Hw sec 7 8a Pdf



Answered Graph Y 4 X 2 3 Using Bartleby



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic



Using Transformations To Graph Functions



Absolute Value Transformations



Content Geometric Transformations Of Graphs Of Functions
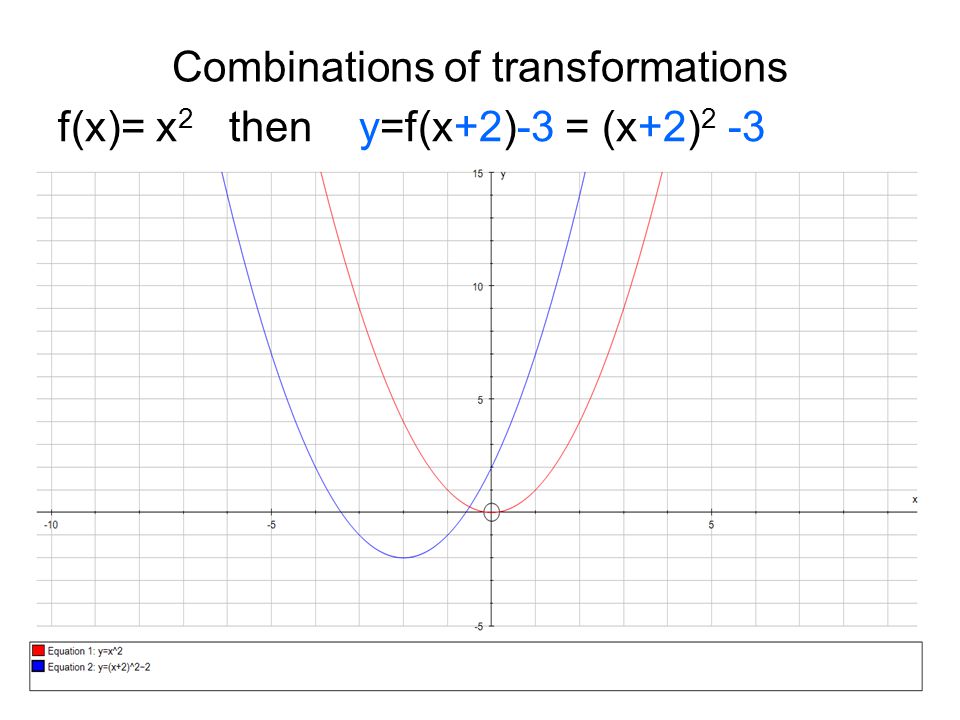



Transformation Of Graphs Andrew Robertson Transformation Of F X A F X X Ppt Download




Which Sequence Of Transformations Produces A Congruent Figure Note Each Answer Choice Represents A Brainly Com




Graph Of Y X 2 Transformations Novocom Top



How Do You Sketch The Graph Of Y X 2 2 2 And Describe The Transformation Socratic




1 07 Transformations Of Functions
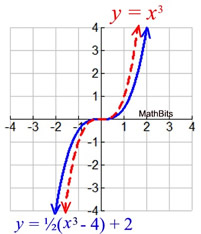



Sequence Of Transformations On Functions Mathbitsnotebook Ccss Math




The Transformation Of The Graph Of A Quadratic Equation Matherudition



Vce School Notes Graph Transformations



1




Graph Using Translations G X X 2 2 1 Transformations Algebra Fwk Ia 02 0501 Youtube
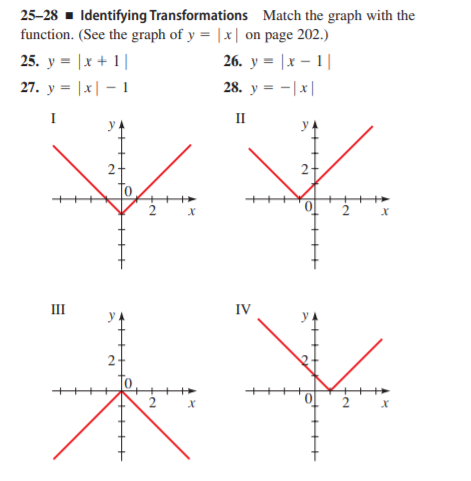



Answered 25 28 Identifying Transformations Bartleby




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Parent Function Worksheet 2



Use Transformations To Graph The Following Quadratic Chegg Com




1 07 Transformations Of Functions



Biomath Transformation Of Graphs




Describe How The Graph Of Y X 2 Can Be Transformed Chegg Com



Investigating Transformations Of Quadratic Graphs International Baccalaureate Maths Marked By Teachers Com




Transformations Of Quadratic Functions College Algebra



Using Transformations To Graph Functions Of The Form



Solution I Have A Question That States A Use The Transformations On The Graph Of Y X 2 To Determine The Graph Of Y X 5 2 9 B Using The Graph Of F X X 2 As A Guide Graph




The Graph Of Y Sqrt 8x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Study Com



Algebra 2 Transformations Of Functions Pt 1 Youtube



Desmos 2 Transformations Of Graphs Cambridge Maths Hub



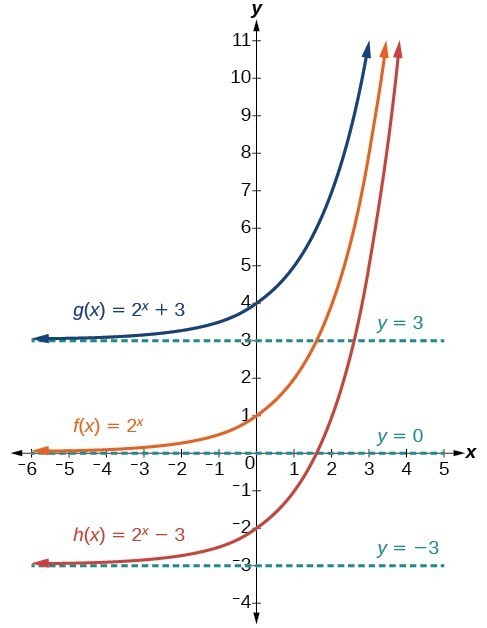
Graph Exponential Functions Using Transformations College Algebra



Transformations Of Y X2 In Vertex Form Organizer And Presentation
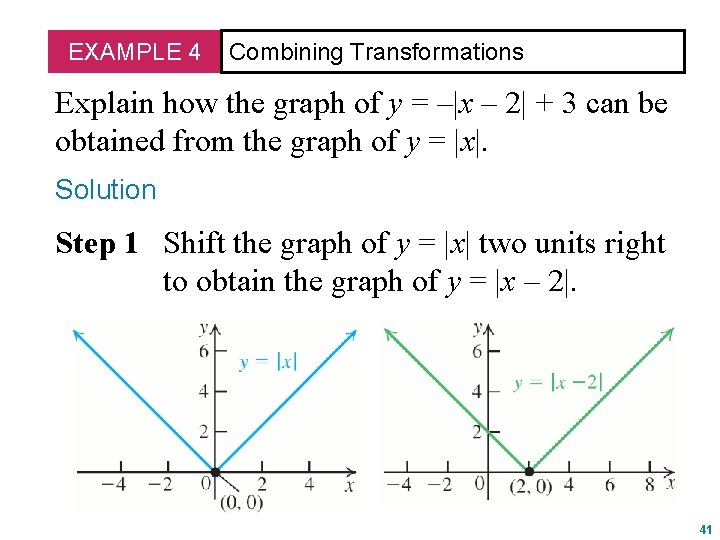



Transformations Of Section Functions 2 7 2 Learn




Sketch The Graph Of The Equation Y X 2 2 3 Study Com



Jdlogo Home Functions Defined Functions You Should Know Transformations Of Quadratics Translations Reflections Inverses Stretches Combinations Combining Functions Review Test Unit 2 Functions And Transformations Lesson 3a
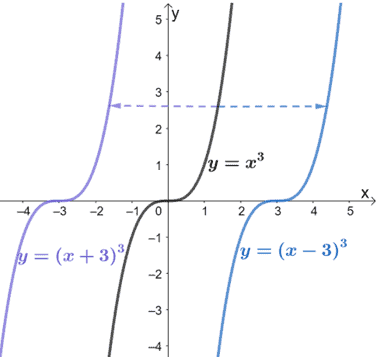



Transformations Of Functions Explanation Examples




Solution Order Order Combining Functions Underground Mathematics




Identifying Vertical Stretch Or Shrink




Functions Transformations Isaac Physics




Combining Transformations Ck 12 Foundation



Function Transformations



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau



0 件のコメント:
コメントを投稿